函数与数学思维品质
湖南省石门县第二中学 曾林
思维品质是指个体思维活动特殊性的外部表现,它包括思维的深刻性、灵活性、敏捷性、批判性和创造性等品质。这些品质相辅相成,密不可分,共同构建完善的思维。
“数学是一门理性思维的科学”,数学教学实质是数学思维活动的教学。在数学教学中,教师要注重学生良好地思维。
函数作为高中数学的主线,贯穿于整个高中数学教学的始终,也是高考的重点和热点。函数的定义域(或变量的允许值范围)是构成函数的三大要素之一,在相关解题教学中应该及时强调定义域(或变量的允许值范围)对解题结论的作用与影响。加深了对定义域的理解和拓展,学生面对疑问尤如有了“北极星”的指引,将不再迷失。这对训练提高学生的数学思维品质是非常有益的环节。
1 应用题
函数关系式包括定义域和对应法则,在求函数的关系式时需要考虑所求函数的定义域。同样,函数的最值是指函数在给定的定义域区间上取到最大(小)值的问题,都需要注意定义域。如:
例1:某工厂拟建一座平面图为矩形且面积为200平方米的三级污水处理池,由于地形限制,长和宽都不能超过16米,如果池外壁建造单价为每平方米400元,中间两条隔墙建造单价为每平方米248元,池底建造单价为每平方米80元(池壁厚度不计,且无池盖)。
|
|
|
①写出总造价 y 元与污水处理池长 x (米)的函数关系式。
②求出污水处理池的长和宽各为多少时,
污水处理池的总造价最低?并求出最低总造价。
错解: ①设污水处理池的长为x米,则宽为![]() 米,总造价
米,总造价
y=![]()
![]() (0<x≤16).
(0<x≤16).
② y![]() ≥
≥![]()
当且仅当 x=![]() 即x=18时取等号,所以最低造价为44800元
即x=18时取等号,所以最低造价为44800元
错因 上述解法的思路是正确的,①中所列的式子也正确,但定义域不严格,应考虑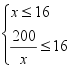 得到
得到![]() ,即问题中的每条线段都要符合实际要求。②中应用不等式解最值时,忽视等号成立的条件为x=18,而在定义域内取不到18,所以应根据函数的单调性进行分析求解
,即问题中的每条线段都要符合实际要求。②中应用不等式解最值时,忽视等号成立的条件为x=18,而在定义域内取不到18,所以应根据函数的单调性进行分析求解
正解: ① y![]() ,
,![]()
②在![]() 时,函数 y 单调递减,所以当
时,函数 y 单调递减,所以当![]() 即长为16米,宽为12.5米时,总造价最低为45000元。
即长为16米,宽为12.5米时,总造价最低为45000元。
这个例子说明,在利用函数解决实际问题时,①要注意到函数定义域的取值范围对实际问题的影响。若考虑不全面,居然与正确答案失之交臂,就体现出思维不深刻。②是若注意到了定义域的变化,又能具体问题具体分析, “一计不成,再施一计”,在学生的解题过程中展示良好的思维灵活性。
2 函数值域
函数的值域是函数值的集合。在求值域时应充分考虑到定义域的作用。如:
例2:已知![]() 的值域
的值域
错解: ∵![]() ∴
∴![]()
∴![]()
![]()
∴![]() 当
当![]() =-1时,A有最大值为
=-1时,A有最大值为![]() .
.
分析:其实不仅要考虑![]() 的范围而且还要考虑
的范围而且还要考虑![]() 的范围,思维要深刻
的范围,思维要深刻
正解:∵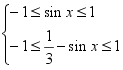 ∴
∴![]()
∴![]() 当
当![]() =
=![]() 时,A有值域为
时,A有值域为![]()
上面例子说明,变量的允许值范围是非常重要的。若能发现变量隐含的要求,精细地检查解题思维的过程,就可以避免以上错误结果的产生。也就是说,学生若在解题过程中,善于找出变量的允许值范围,“飞越误区”,便体现出良好的思维批判性。
3 函数单调性
讨论函数单调性要在定义域区间上进行讨论。判别复合函数单调性时,复合的两个函数在同一区间内的单调性一致时为增函数,单调性相反时为减函数,即“同增异减”。如:
例3:函数![]() 在
在![]() 单调递增,求a的取值范围.
单调递增,求a的取值范围.
错解: 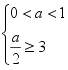 或
或 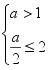
∴![]() 或 1< a ≤4
或 1< a ≤4
∴![]()
分析:当![]() 时,
时, ![]() 是减函数。要使原函数为增函数,则需
是减函数。要使原函数为增函数,则需![]() 在
在![]() 为减函数,故
为减函数,故![]() .这些都考虑到了。但同时也要注意使函数的定义域:
.这些都考虑到了。但同时也要注意使函数的定义域:![]() 即
即![]() .这是初学者最容易忽视的地方。
.这是初学者最容易忽视的地方。
当![]() 时,同样也需要
时,同样也需要![]() .
.
正解: 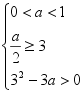 或
或 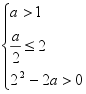
∴![]() 或
或 ![]()
∴![]()
如果在做复合函数题时,没有在定义域内分别考虑两个函数的单调性,就说明学生对复合函数单调性没有理解。对函数单调性概念一知半解,遇到问题时,无法抓住单调性的实质,也说明学生的思维缺乏深刻性。
4 函数奇偶性
判断函数的奇偶性,应先考虑定义域区间是否关于零成中心对称,如果定义域区间关于零不成中心对称,则函数就是非奇非偶函数。否则就用函数奇偶性定义再进一步加以判断。如:
例4:判断函数![]() 的奇偶性.
的奇偶性.
解:∵![]() ∴ 定义域区间[-1,1)关于0不对称
∴ 定义域区间[-1,1)关于0不对称
∴ 函数![]() 是非奇非偶函数.
是非奇非偶函数.
若学生像以上这样的过程进行解答,就很好地体现出解题思维的敏捷性。
变式:判断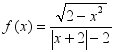 的奇偶性.
的奇偶性.
解:∵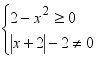 ∴
∴![]()
此时如果直接比较![]() 和
和![]() 有一定困难,容易得非奇非偶的错误结论。可以再利用定义域将原函数化简,使思维更加深刻,有“柳暗花明又一村”的感受,又达到了突破困难的效果,体现出更好的思维敏捷性:
有一定困难,容易得非奇非偶的错误结论。可以再利用定义域将原函数化简,使思维更加深刻,有“柳暗花明又一村”的感受,又达到了突破困难的效果,体现出更好的思维敏捷性:
∵![]() =x+
=x+![]() -
-![]() =x ∴
=x ∴![]() =
=![]() 很容易得出
很容易得出![]() 为奇函数。
为奇函数。
5 函数综合题
例5.定义在R上的偶函数![]() 满足条件:
满足条件:![]() 且在
且在![]() 上单调递减,若
上单调递减,若![]() 是锐角三角形的两内角,以下关系式成立的是
是锐角三角形的两内角,以下关系式成立的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
分析:①由于![]() 是锐角,观察选项知需讨论函数
是锐角,观察选项知需讨论函数![]() 定义
定义![]() 在上的单调性。
在上的单调性。
∵![]() ∴
∴![]() 周期为2
周期为2
又∵![]() 在
在![]() 上单调递减 ∴
上单调递减 ∴![]() 在
在![]() 上单调递减
上单调递减
又∵![]() 在R上是偶函数 ∴
在R上是偶函数 ∴![]() 在
在![]() 上单调递增
上单调递增
②要区分自变量的大小关系。需要寻找恰当的![]() 的关系
的关系
∵![]() ∴
∴![]()
∵![]() 是锐角 ∴
是锐角 ∴![]() 都是锐角
都是锐角
∴![]() 即
即![]() ∴
∴![]() .选择B
.选择B
或取![]() =60°检验得
=60°检验得![]() 而其他关系不成立
而其他关系不成立
∴![]() .选择B
.选择B
本题首先要抓住问题的本质是讨论函数的单调性,特别是要确立单调区间为![]() ,这有助于培养学生思维的敏捷性。在讨论自变量的大小关系时,应进一步结合三个内角都是锐角的要求,寻找恰当的
,这有助于培养学生思维的敏捷性。在讨论自变量的大小关系时,应进一步结合三个内角都是锐角的要求,寻找恰当的![]() 的关系(或值)。这有助于训练学生思维的深刻性。若能考虑选择题型可能不需要充要条件,以“特殊代一般”就能选出正确答案,采用检验排除法解题,则更显思维的灵活性。对比上述两种方法又突出了思维的批判性!以简捷思路解题,就有创造的快感!
的关系(或值)。这有助于训练学生思维的深刻性。若能考虑选择题型可能不需要充要条件,以“特殊代一般”就能选出正确答案,采用检验排除法解题,则更显思维的灵活性。对比上述两种方法又突出了思维的批判性!以简捷思路解题,就有创造的快感!
6 数列
数列是定义在自然数集N范围之内的特殊函数,其通项和前n项和是分段函数关系: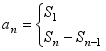
![]() 。如:
。如:
例6:已知数列![]() 的前n项和
的前n项和![]() =9-6n
=9-6n
① 求数列![]() 的通项公式.
的通项公式.
② 设![]() ,求数列
,求数列![]() 的前n项的和
的前n项的和![]() .
.
解:①∵![]() =
=![]() -
-![]() =-6 ∴
=-6 ∴![]() =
=![]()
学生常常这样由于掌握公式不深刻,遗忘公式分两种情况,上面只是![]() 的情形
的情形
应该这样解答:
n=1时, ![]()
![]() =
=![]() , ∴
, ∴![]() =3
=3
![]() 时,
时, ![]() =
=![]() -
-![]() =-6 ∴
=-6 ∴![]() =
=![]()
∴通项公式为![]() =
=![]()
![]()
② n=1时, ![]() =3,
=3, ![]() 时,
时, ![]() =n(n+1)
=n(n+1)
∴![]() =
=![]() ∴
∴![]() =
=![]() =
=![]()
∴![]() …
…![]()
![]() …
…![]()
![]() (
(![]() )
)
当n=1时上式也成立,所以对![]() 上式都成立。
上式都成立。
其它一些数学公式其实也就是一些特殊的函数,在使用公式时也要注意公式成立的条件,也就是要注意函数的定义域:
例如求![]() +
+![]() 的值.
的值.
此题看似缺少条件,事实上暗藏玄机,学生如能以函数的思想理解题意,深化函数概念,敏捷的抓住问题本质:其变量的取值有要求,就能迅速解得。
解:∵
∴n=4,原式=![]() +
+![]() =80640
=80640
在公式教学中要强调完整地掌握公式,加深、扩充对函数概念的理解,逐步理顺知识之间的关联,构建自己的知识体系,同时达到培养完善地思维的目的。
总而言之,在解题时,若能迅速准确理解题意,精细地检查解题思维过程,思辨相应的函数的定义域(或者变量的取值范围)的影响,就能提高学生质疑辨析能力,培养学生综合运用知识解决问题的能力和创造力。在教学中注重加强有关训练,有利于及时提升、完善学生的数学综合思维品质,同时激发学生学习数学的热情。